In this R Notebook I implement an Convolutional Neural Network (CNN) using the MNIST Database for handwritten digits recognition using mxnet framework for R.
Setup
You will need to install the mxnet for R and, if you intent to use your GPU card, the NVidia CUDA Drivers.
Download all four dataset files from MNIST site and gunzip them in the project directory.
Finally, load the libraries.
1
2
3
|
library(mxnet) # ann framework
library(magrittr) # to use modeling the framework
library(caret) # to use to check the performace
|
Loading dataset
We’ll use an adaptation of gist from Brendan o’Connor to read the files transforming them in a structure simple to use and access.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
# read function returns a list of datasets
load_mnist <- function() {
load_image_file <- function(filename) {
ret = list()
f = file(filename,'rb')
readBin(f,'integer',n=1,size=4,endian='big')
ret$n = readBin(f,'integer',n=1,size=4,endian='big')
nrow = readBin(f,'integer',n=1,size=4,endian='big')
ncol = readBin(f,'integer',n=1,size=4,endian='big')
x = readBin(f,'integer',n=ret$n*nrow*ncol,size=1,signed=F)
ret$x = matrix(x, ncol=nrow*ncol, byrow=T)
close(f)
ret
}
load_label_file <- function(filename) {
f = file(filename,'rb')
readBin(f,'integer',n=1,size=4,endian='big')
n = readBin(f,'integer',n=1,size=4,endian='big')
y = readBin(f,'integer',n=n,size=1,signed=F)
close(f)
y
}
train <- load_image_file('./data/train-images.idx3-ubyte')
test <- load_image_file('./data/t10k-images.idx3-ubyte')
train$y <- load_label_file('./data/train-labels.idx1-ubyte')
test$y <- load_label_file('./data/t10k-labels.idx1-ubyte')
return(
list(
train = train,
test = test
)
)
}
# plot one case
show_digit <- function(arr784, col=gray(12:1/12), ...) {
image(matrix(arr784, nrow=28)[,28:1], col=col, ...)
}
# load
mnist <- load_mnist()
|
Let’s check the dataset loaded.
1
2
3
|
labels <- paste(mnist$train$y[1:5],collapse = ", ")
par(mfrow=c(1,5), mar=c(0.1,0.1,0.1,0.1))
for(i in 1:5) show_digit(mnist$train$x[i,])
|
Labels: 5, 0, 4, 1, 9
Convolutional Neural Network
LeNet
In this exercise I’ll use one of the LeNet archictecutre for the neural network, based in two sets of Convolutional filters and poolings and two fully connected layers, as show bellow.
Magrittr
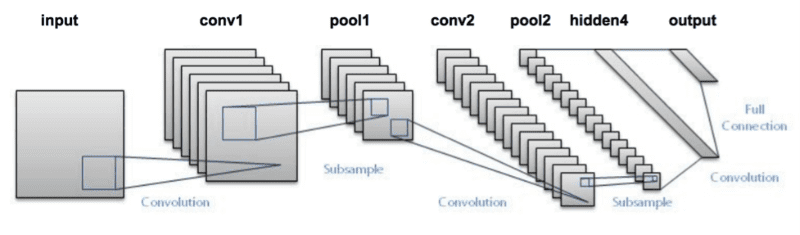
I used the R magrittr pipe operator to build the network in the mxnet, is easer to read the code. But, we’ll check the output of each individual layer and to keep the link with intermediary symbols I declare an assign operator to work in the pipe.
1
2
3
4
5
6
7
|
# pipe assign function
# example: rnorm(5,mean=5) %>% sqrt() %=>% "varname" %>% mean()
"%=>%" <- function(val,var) {
assign(substitute(var),val, envir = .GlobalEnv)
return(val)
}
|
Neural Network
Finnally, lets model the Neural Network.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
# input data
lenet <- mx.symbol.Variable("data") %>%
# Convolutional Layer Set 1 ( Conv > Tanh > Pool )
mx.symbol.Convolution( kernel=c(5,5), num_filter=20, name="Conv1" ) %=>% "Conv1" %>%
mx.symbol.Activation( act_type="tanh", name="Act1" ) %=>% "Act1" %>%
mx.symbol.Pooling( pool_type="max", kernel=c(2,2),
stride=c(2,2), name = "Pool1") %=>% "Pool1" %>%
# Convolutional Layer Set 1 ( Conv > Tanh > Pool )
mx.symbol.Convolution( kernel=c(5,5), num_filter=50 , name="Conv2") %=>% "Conv2" %>%
mx.symbol.Activation( act_type="tanh", name="Act2" ) %=>% "Act2" %>%
mx.symbol.Pooling( pool_type="max", kernel=c(2,2),
stride=c(2,2), name = "Pool2") %=>% "Pool2" %>%
# Flat representation 50 2D filters -> 1D Array
mx.symbol.flatten( name="Flat") %=>% "Flat1" %>%
# Fully Connected Layer 1
mx.symbol.FullyConnected( num_hidden=500, name="Full1" ) %=>% "Full1" %>%
mx.symbol.Activation( act_type="tanh", name="Act3" ) %=>% "Act3" %>%
# Fully Connected Layer 1
mx.symbol.FullyConnected( num_hidden=10 , name="Full2") %=>% "Full2" %>%
mx.symbol.SoftmaxOutput(name="SoftM") %=>% "SoftM"
|
Checking the model built
1
|
graph.viz( lenet, direction = "LR" )
|
Training
We must resize the training and test sets to new archtecture: the training set is a 10000 records of 784 pixel, we must rebuild the 2D (784 -> 28 x 28). Besides this, as we are using convolutional filters, where each image will generate N filter that will be stored in the 3rd dimension, and each case will be stored in the 4th dimension.
So, our dataset will be 4D matrices: 28 x 28 x 1 x 10000.
1
2
3
4
5
6
7
8
9
|
# Resizing the dataset from 10000 x 784 to (28 x 28) x 1 x 100000
# train
tr.x <- t(mnist$train$x)
dim(tr.x) <- c(28,28,1,ncol(tr.x))
# test
ts.x <- t(mnist$test$x)
dim(ts.x) <- c(28,28,1,ncol(ts.x))
|
Finally, traing the network.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
# training
logger.epoc <- mx.callback.log.train.metric(100)
logger.batch <- mx.metric.logger$new()
mx.set.seed(42) # the life, the universe and everything
ti <- proc.time()
model <- mx.model.FeedForward.create(lenet,
X=tr.x,
y=mnist$train$y,
eval.data=list(
data=ts.x,
label=mnist$test$y),
ctx=mx.cpu(),
num.round=20,
array.batch.size=100,
learning.rate=0.05,
momentum=0.9,
wd=0.00001,
eval.metric=mx.metric.accuracy,
epoch.end.callback=logger.epoc,
batch.end.callback=mx.callback.log.train.metric(1, logger.batch))
te <- proc.time()
print(te-ti)
mx.model.save(model, "mnistModel",1)
|
Evaluation
Confusion Matrix
Checking the performance of trained CNN in the test set.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
# process the validation dataset
outputs <- predict(model,ts.x)
# the output is a 10 x 10000 matrix
# transpose to transform in a tidy dataset ( cases x result )
t_outputs <- t(outputs)
# the last layer is a softmax agregator
# so, each column of the dataset is de probability of a value from 0 to 9
# lets get the biggest probability for each test case
y_hat <- max.col(t_outputs)-1 # base index is 1
cm <- confusionMatrix(y_hat,mnist$test$y)
cm$table
|
1
2
3
4
5
6
7
8
9
10
11
12
|
## Reference
## Prediction 0 1 2 3 4 5 6 7 8 9
## 0 974 0 1 0 0 2 3 0 2 0
## 1 1 1131 0 0 0 0 2 2 0 0
## 2 0 0 1025 1 1 0 0 2 0 0
## 3 0 0 0 1000 0 5 1 1 1 2
## 4 0 0 1 0 970 0 0 1 0 6
## 5 1 0 0 6 0 878 4 0 2 2
## 6 3 2 1 0 1 2 947 0 0 1
## 7 1 0 2 0 0 0 0 1016 0 3
## 8 0 2 2 3 0 4 1 1 966 1
## 9 0 0 0 0 10 1 0 5 3 994
|
1
2
3
4
|
## Accuracy Kappa AccuracyLower AccuracyUpper AccuracyNull
## 0.9901000 0.9889958 0.9879601 0.9919467 0.1135000
## AccuracyPValue McnemarPValue
## 0.0000000 NaN
|
Visualizing the worst cases
Worst Case
Let’s find the worst case, where the CNN makes its most prediction errors. To do that, just take the greater value (not in the diagonal) in the confusion matrix.
1
2
3
4
5
6
7
|
# found where the network most fail
errors <- cm$table
diag(errors) <- 0
worst <- which( errors==max(errors), arr.ind = T) - 1
worst
|
1
2
|
## Prediction Reference
## 9 9 4
|
Finding mismatching cases
Let’s see some of these cases were a image labeled as 4 is predicted as 9:
1
2
3
4
5
|
worst.idx <- mnist$test$y == worst[1,"Reference"] & y_hat == worst[1,"Prediction"]
worstcases <- mnist$test$x[worst.idx,]
par(mfrow=c(2,5), mar=c(0.1,0.1,0.1,0.1))
for(i in 1:10) show_digit(worstcases[i,])
|
Indeed some cases are remarkable difficult to identify as 4, so how far the CNN predict the wrong value?
1
2
3
|
wpred <- t_outputs[ worst.idx, ]
par(mfrow=c(2,5), mar=c(0.1,0.1,0.1,0.1))
for(i in 1:10) barplot(wpred[i,])
|
We see some “residual” classification of the number 4 (in the chart, x axis is from 0 to 9).
Inspecting the network layers
Binding and Feed Forward
To visualize the intermediary layers output, first we must “bind” some symbols to the CNN itself, and transfer the learning arguments and parameters.
After that we can perform a feed forward activation and propagation and visualize some outputs in the layers.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
# use the layer's references to build a group symbol
# create an executor to controls the network
out <- mx.symbol.Group(c(Conv1, Act1, Pool1, Conv2, Act2, Pool2, Flat1, Full1, Act3, Full2, SoftM))
executor <- mx.simple.bind(symbol = out, data=dim(ts.x), ctx=mx.cpu())
# transfer the arguments and parameters learned
mx.exec.update.arg.arrays(executor, model$arg.params, match.name = T)
mx.exec.update.aux.arrays(executor, model$aux.params, match.name = T)
# prepare the input
mx.exec.update.arg.arrays(executor, list(data=mx.nd.array(ts.x)), match.name=TRUE)
# Feedforward: propagates the input to output throught the network
mx.exec.forward(executor, is.train=FALSE)
# list the output elements
names(executor$ref.outputs)
|
1
2
3
|
## [1] "Conv1_output" "Act1_output" "Pool1_output" "Conv2_output"
## [5] "Act2_output" "Pool2_output" "Flat_output" "Full1_output"
## [9] "Act3_output" "Full2_output" "SoftM_output"
|
Convolution Layer One
Conv Filters
1
2
3
4
5
6
7
8
9
10
|
# choosing the first worst case
j <- which( worst.idx==T )[1]
# Conv1 Filters
par(mfrow=c(4,5), mar=c(0.1,0.1,0.1,0.1))
for (i in 1:20) {
outputData <- as.array(executor$ref.outputs$Conv1_output)[,,i,j]
image(outputData[,24:1],
xaxt='n', yaxt='n')
}
|
Activation
1
2
3
4
5
6
|
par(mfrow=c(4,5), mar=c(0.1,0.1,0.1,0.1))
for (i in 1:20) {
outputData <- as.array(executor$ref.outputs$Act1_output)[,,i,j]
image(outputData[,24:1],
xaxt='n', yaxt='n')
}
|
Pooling
1
2
3
4
5
6
|
par(mfrow=c(4,5), mar=c(0.1,0.1,0.1,0.1))
for (i in 1:20) {
outputData <- as.array(executor$ref.outputs$Pool1_output)[,,i,j]
image(outputData[,12:1],
xaxt='n', yaxt='n')
}
|
Convolutional Layer Two
Filters
1
2
3
4
5
6
|
par(mfrow=c(7,7), mar=c(0.1,0.1,0.1,0.1))
for (i in 1:49) {
outputData <- as.array(executor$ref.outputs$Conv2_output)[,,i,j]
image(outputData[,8:1],
xaxt='n', yaxt='n')
}
|
Activations
1
2
3
4
5
6
|
par(mfrow=c(7,7), mar=c(0.1,0.1,0.1,0.1))
for (i in 1:49) {
outputData <- as.array(executor$ref.outputs$Act2_output)[,,i,j]
image(outputData[,8:1],
xaxt='n', yaxt='n')
}
|
Pooling
1
2
3
4
5
6
|
par(mfrow=c(7,7), mar=c(0.1,0.1,0.1,0.1))
for (i in 1:49) {
outputData <- as.array(executor$ref.outputs$Pool2_output)[,,i,j]
image(outputData[,4:1],
xaxt='n', yaxt='n')
}
|
Flattering
50 filter of 4 x 4 -> 50 x 16 -> 1 x 800
1
2
3
|
par(mfrow=c(1,1), mar=c(0.1,0.1,0.1,0.1))
outputData <- as.array(executor$ref.outputs$Flat_output)
image(t(matrix(outputData[,j],nrow = 1)), xaxt='n', yaxt='n')
|
Fully Connected Layer
800 -> 500
1
2
3
|
par(mfrow=c(1,1), mar=c(0.1,0.1,0.1,0.1))
outputData <- as.array(executor$ref.outputs$Full1_output)
image( t(matrix(outputData[,j],nrow = 1)) , xaxt='n', yaxt='n')
|
Activation
1
2
3
|
par(mfrow=c(1,1), mar=c(0.1,0.1,0.1,0.1))
outputData <- as.array(executor$ref.outputs$Act3_output)
image( t(matrix(outputData[,j],nrow = 1)) , xaxt='n', yaxt='n')
|
Full Connected Layer 2
1
2
3
4
|
par(mfrow=c(1,1), mar=c(0.1,0.1,0.1,0.1))
outputData <- as.array(executor$ref.outputs$Full2_output)
outputData <- t(matrix(outputData[,j],nrow = 1))
image( outputData, xaxt='n', yaxt='n')
|
Activation
1
2
3
4
|
par(mfrow=c(1,1), mar=c(0.1,0.1,0.1,0.1))
outputData <- as.array(executor$ref.outputs$SoftM_output)
outputData <- t(matrix(outputData[,j],nrow = 1))
image( outputData, xaxt='n', yaxt='n')
|
